联系我们
勒克斯之家资讯
分析离心油泵性能的新方法:
发布者:haitan 发布时间:2013-11-12 09:43:16 访问次数:263
分析离心泵水力性能有三个层次。第一个层次是宏观层次,即通常的外特性,如:扬程、轴功率和效率与流量的关系。第二个层次是中间层次,即那些与泵水力设计息息相关的综合性流动参数,如:滑移系数、水力效率、容积效率、机械效率和水力损失系数等。第三个层次是微观层次,即泵的内特性,如:叶轮、吸入室和压出室等过流部件内部流场特性。目前对第一、三层次研究比较多,并试图建立两者的定量关系。对第二层次研究进行得相当少。本文旨在给出一种由泵外特性推算出中间层次流动参数的方法。通过洞察不同粘度下这些参数随叶片数的变化,来深入评价被输送液体粘度对离心油泵性能的影响,为离心油泵的水力设计提供依据,并指明研究方向。 1.1 离心油泵的性能 扬程-流量、轴功率-流量和效率-流量曲线表示离心油泵的水力性能,一般用只能采用实验的方法才能得到性能,见图1。本文试图分析出最优工况的滑移系数、水力效率、容积效率、机械效率和水力损失系数等参数。
1.2 泵内部水力损失 根据流体力学理论,在最优工况下,泵过流部件内部水力损失主要是沿程摩擦阻力损失,局部旋涡损失和冲击损失所占比重相当小,可以忽略不计。于是得到泵内部流动能量平衡关系式:
1 分析方法:
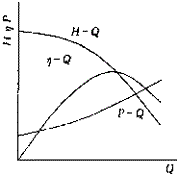 图1 离心油泵性能曲线
H=Hth-KQ2
式中:H为已知的最优工况扬程,Hth为最优工况理论扬程,Q为已知的最优工况流量,K为水力损失系数,其中Hth、K由实验数据推算。
根据性能实验结果,已经做出了扬程-流量曲线。于是,下式成立
dH/dQ=dHth/dQ-2KQ
式中:最优工况扬程曲线斜率dH/dQ由实验曲线求取。 在忽略叶轮进口预旋的情况下,离心泵基本方程为 Hth=Vu2u2/g
叶轮出口液体绝对速度的圆周分速度为 Vu2=σu2-Q/ηVA2tanβ2
式中:σ为最优工况滑移系数,σu2表示考虑滑移速度后的叶轮圆周速度,ηV为最优工况泵容积效率,A2为叶轮出口面积,β2为叶片出口角,u2为叶轮圆周速度。 于是理论扬程为
将该式对Q求导,得到
dHth/dQ=-u2/gηVAstanβ2
联立求解方程(1)、(2)、(5)和(6),得到滑移系数
水力损失系数
水力效率
ηh=H/Hth
其中Hth=H+KQ2。
机械效率 ηm=η/ηVηh
其中η为实验测得的泵最优工况的效率。
利用文献[1]的方法计算叶轮前口环同心圆柱面间隙的泄漏损失。叶轮后口环与前口环尺寸相同,后盖板上开有平衡孔,平衡孔有节流作用,所以后口环的泄漏损失比前口环小,暂且假设后口环的泄漏损失为前口环的70%。于是,得到总的泄漏损失 式中:dm为密封环直径,lm为密封环长度,bm为密封环单侧间隙,腍为密封环两侧压力差,其值为,其中:um为口环的圆周速度。
于是可以计算出容积效率
ηV=Q/Q+q
由此可见,利用泵的性能曲线和叶轮有关尺寸,就可以推算出最优工况的滑移系数、水力损失系数、水力效率、容积效率、机械效率。运用该方法可以深入地分析叶轮几何参数对这些参数的影响,更容易看清问题的本质。
2 结果与讨论
2.1 已知数据 本文采用文献[2]叶轮几何尺寸和性能实验数据。有关实验泵、实验装置和实验液体等详细情况见文献[2]。
2.2 滑移系数 图2(a)给出了输送清水时本文计算的滑移系数随叶片数的变化曲线。为了便于对比,图中还给出了利用准三元流动程序计算的滑移系数以及Stodola、Wiesner经验公式计算滑移系数值。图2(b)表示输送清水时最优工况扬程随叶片数的变化。Stodola经验公式为
σ=1-πsinβ2/Z
|
来源:永嘉县海坦泵业有限公司
免责声明:勒克斯之家转载作品均注明出处,本网未注明出处和转载的,是出于传递更多信息之目的,并不意味 着赞同其观点或证实其内容的真实性。如转载作品侵犯作者署名权,或有其他诸如版权、肖像权、知识产权等方面的伤害,并非本网故意为之,在接到相关权利人通知后将立即加以更正。联系电话:0571-87774297。